鐵人賽 Day 18 什麼是「魔改算法」?以MD5為例深度剖析

本系列文章所討論的 JavaScript 資安與逆向工程技術,旨在分享知識、探討防禦之道,並促進技術交流。
所有內容僅供學術研究與學習,請勿用於任何非法或不道德的行為。
讀者應對自己的行為負完全責任。尊重法律與道德規範是所有技術人員應共同遵守的準則。
什麼是魔改算法
在資安與逆向工程領域中,魔改算法指的是對既有的演算法進行修改,讓其輸出的內容與原始標準版本不同。
這種修改通常是為了混淆保護或增加逆向難度,讓攻擊者難以直接利用現成工具進行分析。
MD5原始碼
以下是使用JavaScript產生MD5的原始碼。
function md5(str) {
function rotateLeft(lValue, iShiftBits) {
return (lValue << iShiftBits) | (lValue >>> (32 - iShiftBits));
}
function addUnsigned(lX, lY) {
const lX4 = (lX & 0x40000000);
const lY4 = (lY & 0x40000000);
const lX8 = (lX & 0x80000000);
const lY8 = (lY & 0x80000000);
let lResult = (lX & 0x3FFFFFFF) + (lY & 0x3FFFFFFF);
if (lX4 & lY4) return (lResult ^ 0x80000000 ^ lX8 ^ lY8);
if (lX4 | lY4) {
if (lResult & 0x40000000) {
return (lResult ^ 0xC0000000 ^ lX8 ^ lY8);
} else {
return (lResult ^ 0x40000000 ^ lX8 ^ lY8);
}
}
return (lResult ^ lX8 ^ lY8);
}
function F(x, y, z) { return (x & y) | ((~x) & z); }
function G(x, y, z) { return (x & z) | (y & (~z)); }
function H(x, y, z) { return (x ^ y ^ z); }
function I(x, y, z) { return (y ^ (x | (~z))); }
function FF(a, b, c, d, x, s, ac) {
a = addUnsigned(a, addUnsigned(addUnsigned(F(b, c, d), x), ac));
return addUnsigned(rotateLeft(a, s), b);
}
function GG(a, b, c, d, x, s, ac) {
a = addUnsigned(a, addUnsigned(addUnsigned(G(b, c, d), x), ac));
return addUnsigned(rotateLeft(a, s), b);
}
function HH(a, b, c, d, x, s, ac) {
a = addUnsigned(a, addUnsigned(addUnsigned(H(b, c, d), x), ac));
return addUnsigned(rotateLeft(a, s), b);
}
function II(a, b, c, d, x, s, ac) {
a = addUnsigned(a, addUnsigned(addUnsigned(I(b, c, d), x), ac));
return addUnsigned(rotateLeft(a, s), b);
}
function encodeUTF8(str) {
if (typeof TextEncoder !== "undefined") {
return new TextEncoder().encode(str);
}
const bytes = [];
for (let i = 0; i < str.length; i++) {
let code = str.charCodeAt(i);
if (0xD800 <= code && code <= 0xDBFF && i + 1 < str.length) {
const next = str.charCodeAt(++i);
if (0xDC00 <= next && next <= 0xDFFF) {
code = ((code - 0xD800) << 10) + (next - 0xDC00) + 0x10000;
} else {
i--;
}
}
if (code <= 0x7F) bytes.push(code);
else if (code <= 0x7FF) {
bytes.push(0xC0 | (code >> 6));
bytes.push(0x80 | (code & 0x3F));
} else if (code <= 0xFFFF) {
bytes.push(0xE0 | (code >> 12));
bytes.push(0x80 | ((code >> 6) & 0x3F));
bytes.push(0x80 | (code & 0x3F));
} else {
bytes.push(0xF0 | (code >> 18));
bytes.push(0x80 | ((code >> 12) & 0x3F));
bytes.push(0x80 | ((code >> 6) & 0x3F));
bytes.push(0x80 | (code & 0x3F));
}
}
return new Uint8Array(bytes);
}
function bytesToWords(bytes) {
const words = [];
for (let i = 0; i < bytes.length; i++) {
words[i >> 2] = (words[i >> 2] || 0) | (bytes[i] << ((i % 4) * 8));
}
return words;
}
function binl2hex(binarray) {
const hex_tab = "0123456789abcdef";
let str = "";
for (let i = 0; i < binarray.length * 4; i++) {
str += hex_tab.charAt((binarray[i >> 2] >> (((i % 4) * 8) + 4)) & 0xF) +
hex_tab.charAt((binarray[i >> 2] >> (((i % 4) * 8))) & 0xF);
}
return str;
}
function binl_md5(x, bitLen) {
x[bitLen >> 5] |= 0x80 << (bitLen % 32);
x[(((bitLen + 64) >>> 9) << 4) + 14] = bitLen;
let a = 1732584193;
let b = -271733879;
let c = -1732584194;
let d = 271733878;
for (let i = 0; i < x.length; i += 16) {
let olda = a;
let oldb = b;
let oldc = c;
let oldd = d;
a = FF(a, b, c, d, x[i + 0], 7, -680876936);
d = FF(d, a, b, c, x[i + 1], 12, -389564586);
c = FF(c, d, a, b, x[i + 2], 17, 606105819);
b = FF(b, c, d, a, x[i + 3], 22, -1044525330);
a = FF(a, b, c, d, x[i + 4], 7, -176418897);
d = FF(d, a, b, c, x[i + 5], 12, 1200080426);
c = FF(c, d, a, b, x[i + 6], 17, -1473231341);
b = FF(b, c, d, a, x[i + 7], 22, -45705983);
a = FF(a, b, c, d, x[i + 8], 7, 1770035416);
d = FF(d, a, b, c, x[i + 9], 12, -1958414417);
c = FF(c, d, a, b, x[i + 10], 17, -42063);
b = FF(b, c, d, a, x[i + 11], 22, -1990404162);
a = FF(a, b, c, d, x[i + 12], 7, 1804603682);
d = FF(d, a, b, c, x[i + 13], 12, -40341101);
c = FF(c, d, a, b, x[i + 14], 17, -1502002290);
b = FF(b, c, d, a, x[i + 15], 22, 1236535329);
a = GG(a, b, c, d, x[i + 1], 5, -165796510);
d = GG(d, a, b, c, x[i + 6], 9, -1069501632);
c = GG(c, d, a, b, x[i + 11], 14, 643717713);
b = GG(b, c, d, a, x[i + 0], 20, -373897302);
a = GG(a, b, c, d, x[i + 5], 5, -701558691);
d = GG(d, a, b, c, x[i + 10], 9, 38016083);
c = GG(c, d, a, b, x[i + 15], 14, -660478335);
b = GG(b, c, d, a, x[i + 4], 20, -405537848);
a = GG(a, b, c, d, x[i + 9], 5, 568446438);
d = GG(d, a, b, c, x[i + 14], 9, -1019803690);
c = GG(c, d, a, b, x[i + 3], 14, -187363961);
b = GG(b, c, d, a, x[i + 8], 20, 1163531501);
a = GG(a, b, c, d, x[i + 13], 5, -1444681467);
d = GG(d, a, b, c, x[i + 2], 9, -51403784);
c = GG(c, d, a, b, x[i + 7], 14, 1735328473);
b = GG(b, c, d, a, x[i + 12], 20, -1926607734);
a = HH(a, b, c, d, x[i + 5], 4, -378558);
d = HH(d, a, b, c, x[i + 8], 11, -2022574463);
c = HH(c, d, a, b, x[i + 11], 16, 1839030562);
b = HH(b, c, d, a, x[i + 14], 23, -35309556);
a = HH(a, b, c, d, x[i + 1], 4, -1530992060);
d = HH(d, a, b, c, x[i + 4], 11, 1272893353);
c = HH(c, d, a, b, x[i + 7], 16, -155497632);
b = HH(b, c, d, a, x[i + 10], 23, -1094730640);
a = HH(a, b, c, d, x[i + 13], 4, 681279174);
d = HH(d, a, b, c, x[i + 0], 11, -358537222);
c = HH(c, d, a, b, x[i + 3], 16, -722521979);
b = HH(b, c, d, a, x[i + 6], 23, 76029189);
a = HH(a, b, c, d, x[i + 9], 4, -640364487);
d = HH(d, a, b, c, x[i + 12], 11, -421815835);
c = HH(c, d, a, b, x[i + 15], 16, 530742520);
b = HH(b, c, d, a, x[i + 2], 23, -995338651);
a = II(a, b, c, d, x[i + 0], 6, -198630844);
d = II(d, a, b, c, x[i + 7], 10, 1126891415);
c = II(c, d, a, b, x[i + 14], 15, -1416354905);
b = II(b, c, d, a, x[i + 5], 21, -57434055);
a = II(a, b, c, d, x[i + 12], 6, 1700485571);
d = II(d, a, b, c, x[i + 3], 10, -1894986606);
c = II(c, d, a, b, x[i + 10], 15, -1051523);
b = II(b, c, d, a, x[i + 1], 21, -2054922799);
a = II(a, b, c, d, x[i + 8], 6, 1873313359);
d = II(d, a, b, c, x[i + 15], 10, -30611744);
c = II(c, d, a, b, x[i + 6], 15, -1560198380);
b = II(b, c, d, a, x[i + 13], 21, 1309151649);
a = II(a, b, c, d, x[i + 4], 6, -145523070);
d = II(d, a, b, c, x[i + 11], 10, -1120210379);
c = II(c, d, a, b, x[i + 2], 15, 718787259);
b = II(b, c, d, a, x[i + 9], 21, -343485551);
a = addUnsigned(a, olda);
b = addUnsigned(b, oldb);
c = addUnsigned(c, oldc);
d = addUnsigned(d, oldd);
}
return [a, b, c, d];
}
const bytes = encodeUTF8(str);
const words = bytesToWords(bytes);
const hashWords = binl_md5(words, bytes.length * 8);
return binl2hex(hashWords);
}修改預定義的常數
我們可以在binl_md5核心計算邏輯中看到有非常多預定義的常數。
如 -680876936, -389564586, 606105819 ...等等。
我們可以通過修改這些數字導致最終生成的結果產生變化。
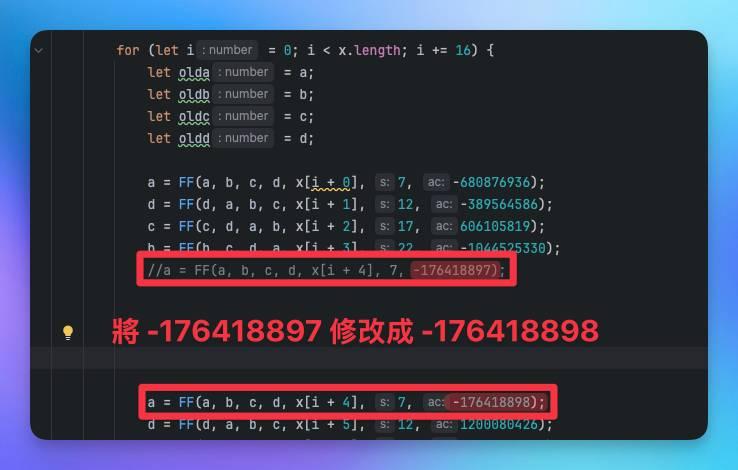
對比輸出值
正常的MD5
const md5Hash = md5("這是一段需要雜湊的訊息")
console.log(md5Hash);
// 6779e90032670bfaae8c7a97af40dc8f魔改過的MD5
const md5Hash = md5("這是一段需要雜湊的訊息")
console.log(md5Hash);
// 00d826c09766875dceadda82740af337魔改算法在常見於 API 驗證、APP 授權、防止盜版或爬蟲等場景。
它並不是比標準算法更安全,而是一種「混淆 + 增加逆向難度」的技巧。
對逆向工程人員來說攻克魔改算法的挑戰在於辨識魔改點並逐步還原,這也是資安實戰中有趣的部分。